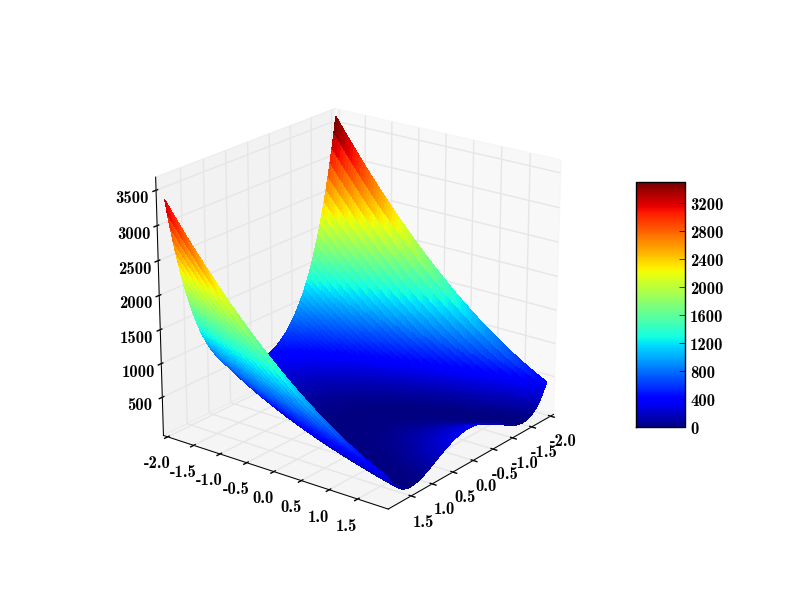
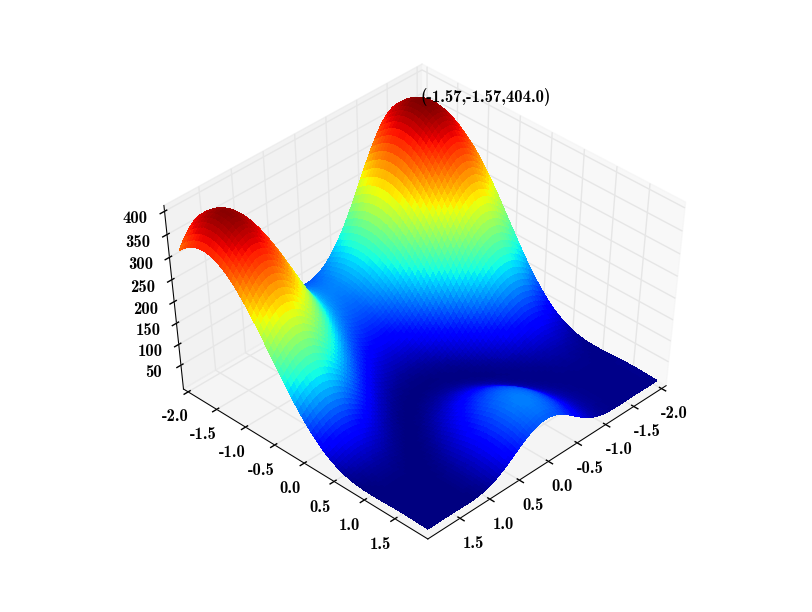
android传输协议以及应用内存限制修改
2013年8月20日 01:13
一直用塞班的系统,这一阵子要做个Android的应用,不熟悉Android导致各种蛋疼。
Android传输协议&AirDroid
习惯了Ubuntu,于是就在Ubuntu下用eclipse开发。首先遇到的就是文件传输的问题。想看看在sd卡中存的文本文件,怎么都找不到在哪儿。Android和电脑之间的传输协议有两种——MTP,PTP。
PTP——图片传输协议(picture transfer protocol)”。最早由柯达公司与微软协商制定的一种标准,符合这种标准的图像设备在接入Windows XP系统之后可以更好地被系统和应用程序所共享,尤其在网络传输方面,系统可以直接访问这些设备用于建立网络相册时图片的上传、网上聊天时图片的传送等。(来自百度百科)
MTP——媒体传输协议(即通常所说的MTP)是“Windows Media”框架的一部分。Windows Vista中内置了对MTP的支持,Mac以及Linux系统有相应的软件包提供对MTP的支持。(来自维基百科)
看了两个协议的简介,实在想不明白,作为世界级的Google公司用了Linux的内核竟然还会用和Windows扯上这么大关系的传输协议!![]() 本以为手机接上Ubuntu可以很简单的mount上去,然后用shell管理的,看样子是泡汤了。
本以为手机接上Ubuntu可以很简单的mount上去,然后用shell管理的,看样子是泡汤了。
后来见有人推荐airDroidhttp://web.airdroid.com/,用了下,感觉很方便,能很好的解决我的需求。因为只是查看下文本文件速度也就不成问题了。这里对于个子较小的文本文件如果能在浏览器中打开就更好了,免得要下载再查看。
应用程序最大内存限制 heap growth limit
由于这个应用要做比较多的图像处理和显示,老是出现 Out of Memory的错误导致程序退出。起初以为是手机内存不够的原因,于是关了很多正在运行的其他程序以及后台服务,发现还是崩 。
。
使用DDMS监视了下内存使用,发现heap size 60M左右的时候就有很大几率挂。突然想起来,java虚拟机有内存使用上限的限制。
google了下,发现有三个变量和java虚拟机内存使用限制有关
dalvik.vm.heapgrowthlimit #单个应用程序最大内存限制 dalvik.vm.heapstartsize #应用启动后分配的初始内存 dalvik.vm.heapsize #单个java虚拟机最大的内存限制
于是执行
adb shell getprop | grep heapgrowthlimit
果然,每个应用内存限制是64M (对于不同的机器这个数字会不一样)。这个参数被纪录在/system/build.prop中。使用adb shell进入手机shell(前提是你的手机正确连上电脑了呀)。很惊奇的发现,Android上的linux还有vi,虽然没有vim有点可惜,不过vi对于我这种菜鸟来说已经足够用了。兴致勃勃冲上去,把/system/build.prop中
(对于不同的机器这个数字会不一样)。这个参数被纪录在/system/build.prop中。使用adb shell进入手机shell(前提是你的手机正确连上电脑了呀)。很惊奇的发现,Android上的linux还有vi,虽然没有vim有点可惜,不过vi对于我这种菜鸟来说已经足够用了。兴致勃勃冲上去,把/system/build.prop中
dalvik.vm.heapgrowthlimit=64m
改成
dalvik.vm.heapgrowthlimit=128m
发现不能保存,报了一个如下的错
"build.prop" File is read only
(这个地方记得不是太清楚是这个错还是Permission denied,反正在此重复试验过程的时候是这个错。我感觉好像是权限的错)。
接着把手机root了后su一下,再改,发现还是有read only的错。
read only解决方案
google 了几个方案,试了下,如下的方法可用
进入android的linux shell后,执行
mount
查看挂载的设备,发现有如下一条:
/dev/block/mmcblk0p9 /system ext4 ro,relatime,errors=panic,barrier=1,data=writeback 0 0
从上面可以看出,挂载点/system挂载的是一个ext4文件系统,relatime何意暂时不知,ro是read only的意思,后面几个参数和ext4的安全性有关,不用太关心。最重要的是ro。执行下面指令,重新挂载这个块设备,设置为可读可写
mount -o remount -o rw /system
这时候你再mount一下,发现原先的ro变成了如下的rw
/dev/block/mmcblk0p9 /system ext4 rw,relatime,errors=panic,barrier=1,data=writeback 0 0
这时候你su一下,再用vi修改/system/build.prop就可以修改了。然后重启一下手机,就ok了。同时也解决了之前用linux 命令随意“进出”android的想法。