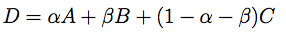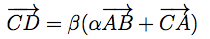之前也接触过遗传算法,只是没有实践,正巧这次模式识别的课程上老师提到,并布置了一个小练习题,便拿来做做吧。
题目本来要求是求Rosenbrock函数f(x, y) = (x-1)2 + 100(y-x2)2在[-2,-2,2,2]之间的最大值,稍加分析,或者看下面的图就会发现,其实当(x, y) = (-2, -2)时,f(x,y)即可取到最大值。
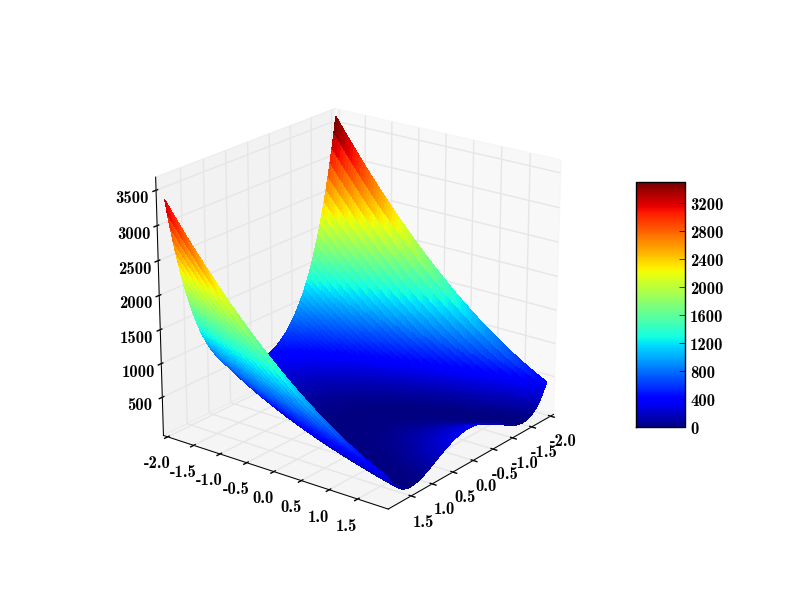
觉得这样没什么意思,于是自己稍微把题目改了下,把x,y都变成sin x,sin y,函数就变成f(x, y) = (sin x-1)2 + 100(sin y-sin2x)2
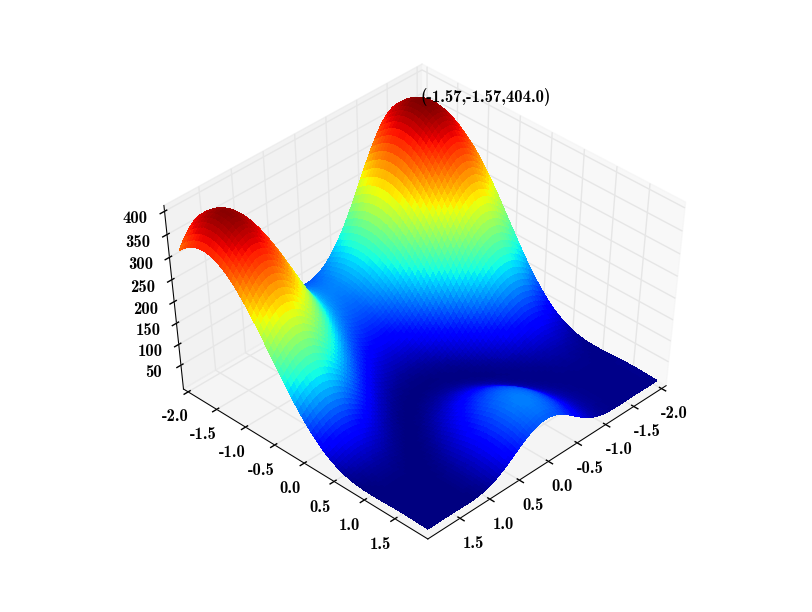
这是一个很漂亮的双峰函数。下面我们来讨论如何用遗传算法来求这个函数的极大值。
编码方式
由于x,y的范围都是[-2,2],那么可以考虑使用11个二进制的定点小数来编码0.000到2.047这2048个定点小数。在加上1个二进制位符号为,即可表示[-2.047, 2.047],刚好可以覆盖[-2,2]并且精度为0.001。x和y都采用相同的方法编码,然后拼接在一起,形成一个24位的二进制整数。实现过程中可以使用整数保存,位运算做遗传和变异。
原始个体生成方式
根据编码方式,每一个个体可以用24个二进制位表示,于是可以很简单的随机生成一个[0,1<<24)的整数表示一个个体。生成30个祖先个体
确定遗传、变异方式
遗传方式:任取两个个体(A,B)进行交配,生成两个子个体(C,D)。C基因序列的低k个二进制位来自于A,高24-k个二进制位来自于另一个父本B,其中0<k<24。D基因序列和C的情况真好相反,其低k个二进制位来自于B,高24-k个二进制位来自于A。用python语言表示为
k = randint(1, 23)
mask = (1<<k) - 1
C = A & mask | B & ~mask
D = B & mask | A & ~mask
变异方式:随机选取24个二进制位中的某一个,如果该位0变成则变成1,否则变成0
确定遗传
在元素个体,遗传得到的个体和变异个体中选取最好的30个个体(对应的函数值最大的30个个体)作为下一次迭代的父样本。
from random import randint
from numpy import sin
def decode(g):
return [((g&0xfff) - 2048) * 0.001, ((g>>12) - 2048) * 0.001]
def function_g(g):
x = decode(g)
return function(x[0], x[1])
def function(x, y):
return 100 * (sin(x) ** 2 - sin(y)) ** 2 + (1 - sin(x)) ** 2
def cmp(g1, g2):
key = function_g(g1) - function_g(g2)
if key > 0: return 1
elif key < 0: return -1
else: return 0
def GA(num = 30, round = 10):
gene = [randint(0, (1<<24) - 1) for i in range(num)]
rnd = 0
while rnd < round:
rnd += 1
gene_c = [g ^ (1<<randint(0, 23)) for g in gene]
gene_h = []
for g1 in gene:
for g2 in gene:
mask = (1<<randint(1, 23)) - 1
gene_h.append(g2 & ~mask | g1 & mask)
gene_h.append(g1 & ~mask | g2 & mask)
gene_tot = gene + gene_h + gene_c
gene_tot.sort(cmp = cmp, reverse = True)
gene = gene_tot[:num]
print "round", rnd, ":", decode(gene[0]), function_g(gene[0])
return decode(gene[0]) + [function_g(gene[0])]
if __name__ == '__main__':
print GA(30, 10),
结果
经过10得到如下结果, 每一行的三个数字分别对应x, y, f(x, y)
round 1 : [1.571, -1.464] 397.724305554
round 2 : [1.571, -1.539] 399.797824716
round 3 : [-1.605, -1.548] 403.426161017
round 4 : [-1.605, -1.556] 403.486264841
round 5 : [-1.541, -1.591] 403.561685598
round 6 : [-1.541, -1.575] 403.639747518
round 7 : [-1.573, -1.579] 403.984587994
round 8 : [-1.573, -1.571] 403.998039526
round 9 : [-1.569, -1.571] 403.998694536
round 10 : [-1.569, -1.571] 403.998694536
可以看到,结果收敛得非常快,并且经过10次迭代,结果基本稳定。
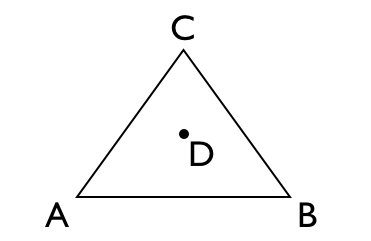
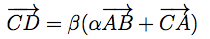 或者
或者