c++11, shared_ptr使用数组
2014年8月19日 21:52
最近被项目垃圾的内存管理搞的特别头大，正好这段时间在看《深入理解C++11：C++11新特性解析与应用》，了解了些c++11的特性。于是想着用c++11高大上的智能指针来做内存管理。
所谓高大上，相对于各种天生就支持垃圾回收的语言（如：java，python）来说也是个废才。支持个数组都麻烦的很，各方考证，下面写一个关于 shared_ptr 使用数组的小样例，主要参考 http://stackoverflow.com/questions/14957359/problems-with-shared-ptrt-wrapping-a-dynamic-array
基于shared_ptr的vector
下面是一个基于shared_ptr的vector模板。当然完全没有必要使用 shared_ptr去实现vector，vector的内存管理本来就是透明的。这个地方就是为了展示shared_ptr怎么使用数组。
template <class T>
class Vector {
shared_ptr<T> ptr_;
int size_, capacity_;
public:
Vector()
:ptr_(shared_ptr<T>(new T[initial_capacity], std::default_delete<T[]>())),
capacity_(initial_capacity), size_(0) {}
int size() const {
return size_;
}
void push_back(const T &x) {
if (size_ == capacity_) {
capacity_ *= 2;
T* new_memory = new T[capacity_];
for (int i = 0; i < size_; ++i) {
new_memory[i] = ptr_.get()[i];
}
ptr_ = shared_ptr<T>(new_memory, std::default_delete<T[]>());
}
ptr_.get()[size_++] = x;
}
const T& operator[] (int idx) const {
return ptr_.get()[idx];
}
T& operator[] (int idx) {
return ptr_.get()[idx];
}
static const int initial_capacity = 2;
};
这里有两个必须要注意的地方
-
除了使用指向内存的指针初始化 shared_ptr外，还需要传入析够数组的函数。不然当内存的引用数降到0时，会调用 delete 释放一个数组，直接导致程序崩溃，std::default_delete<T[]>()指明调用的是 delete[]
shared_ptr<T>(new T[size], std::default_delete<T[]>());
-
既然没有直接支持数组，shared_ptr 也就没有重载 operator [] 了。查看相关文档https://gcc.gnu.org/onlinedocs/gcc-4.6.0/libstdc++/api/a00267.html才知道，shared_ptr 只支持了两个 operator，外加一个获取内存指针的get方法
std::add_lvalue_reference< _Tp >::type operator* () const _Tp * operator-> () const; _Tp * get () const;
因此想要通过下标访问数组元素就可以使用get() 获取原始数组指针，然后使用[]访问，或者直接把这个操作封装起来T& operator[] (int idx) { return ptr_.get()[idx]; }
简单的测试
最后写一个简单的测试程序测试下 Vector 是不是能够zhe，测试程序如下：
class Point {
public:
Point(int x = 0, int y = 0) { ++counter_; }
~Point() { --counter_; }
static int counter() { return counter_; }
int x, y;
private:
static int counter_;
};
int Point::counter_ = 0;
void test_function() {
Vector<Point> vec;
Point p;
for (int i = 0; i < 4; ++i) {
p.x = i;
vec.push_back(p);
}
cout << vec[vec.size() - 1].x << endl;
}
int main(int argc, const char * argv[]) {
test_function();
cout << Point::counter() << endl;
return 0;
}
测试程序输出如下：
3 0
最后一行输出0，说明 test_function函数退出后 Point 类全部析够，正常！
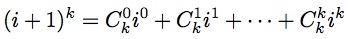
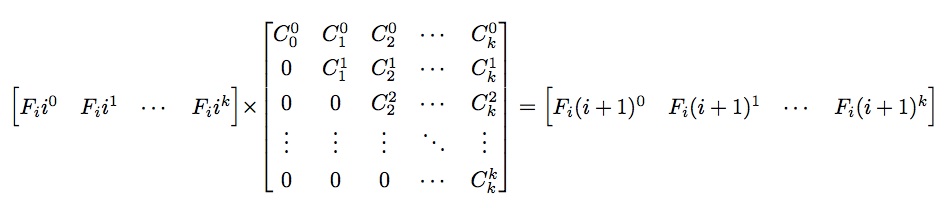
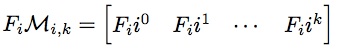
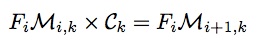
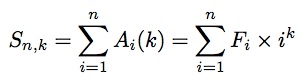
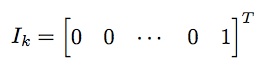
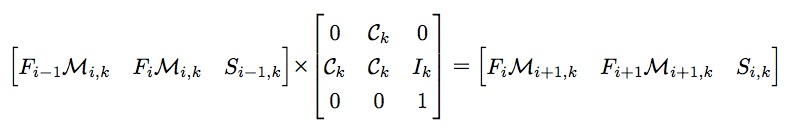
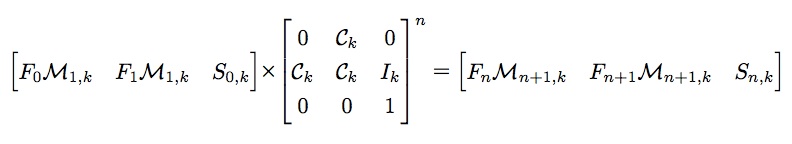
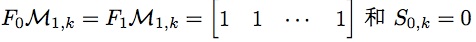
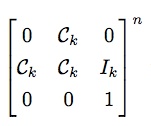部分由矩阵快速幂求解。时间复杂度为O((2k + 3)3 log n)=O(k3 log n)。矩阵快速幂后乘以初值即可得到答案。
