三角形,圆内等概率随机生成一个点
三角形内随机生成一个点
在三角形内生成一个点
已有一个能生成0到1之间的数,并且这些数是均匀分布的随机生成器,给定一个任意的三角形,如何能在三角形内随机的生成一个点?
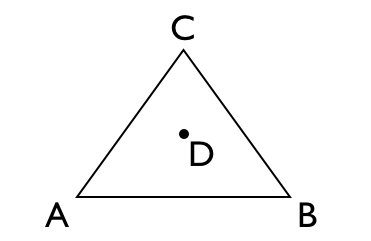
如上面这个三角形,点D就是三角形内部随机的一个点。一种简单的方法是通过如下公式生成D点:
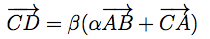 或者
或者
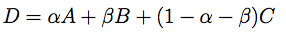
其中,a和b是两个独立随机生成器
要求等概率的情况
以上的两个公式很好的解决了在三角形内随机生成一个点的问题。然而三角形内每一个点被取到的概率一样吗?
拿
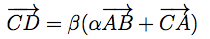
来说。a和b从0开始,每隔1/n取一个点。但n=3时,a和b的取值为{0, 1/3, 2/3, 1},将取到的D点在三角形种标出,如下图
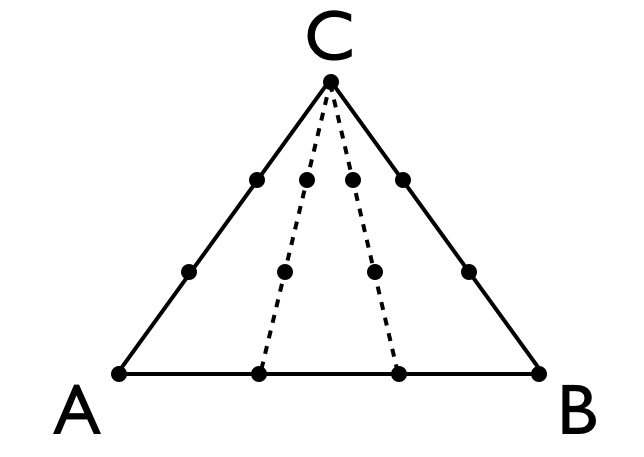
很明显,靠近C点的地方D取值的概率更大。但n趋近于正无穷的时候,上面的图就是D取值的概率密度函数。很显然,三角形内每一个点被取到的概率并不相等。
为了克服这个问题,一名睿智的同学提出了如下的方法:
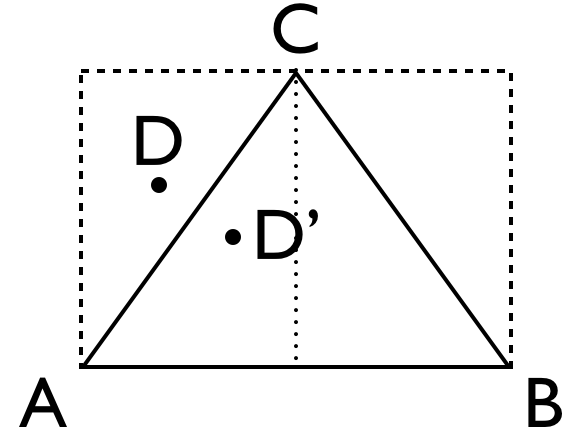
-
将三角形扩充成一个矩形
-
将矩形的两条边分别线性映射成一个随机生成器,这两个随机生成器相互独立
-
如果生成的D点在三角形外,将D以靠近的边为对称轴映射到三角形内的D'上。
显然随机生成的点在矩形内的分布是等概率的,第3部的映射也是一一对应的,因此在三角形内生成的点也是均匀分布的。
多边形内随机生成一个点
多边形可以先分割成多个三角形。根据面积的比率,使用一次随机生成器确定点落在哪个三角形内。然后在使用上面的方法在三角形内随机生成一个点。
圆内随机生成一个点
给定一个半径为R的圆,如何在圆内等概率随机生成一个点?
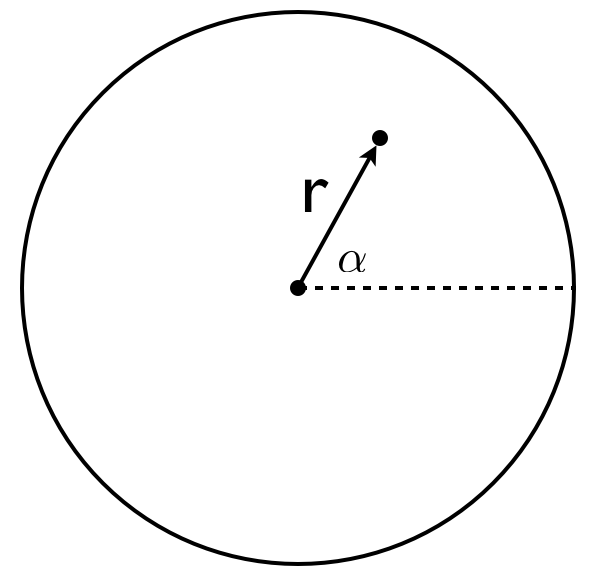
圆用笛卡尔坐标系很不好处理,自然想到使用极坐标系。a表示OD与极轴的夹角,r表示D到坐标原点的距离。a从0度到360度,r从0到R。
如果将a和r直接线性映射到两个独立的随机生成器上。很明显圆内的概率密度函数并不相等。
当r为一个定值,D的轨迹为一个圆,圆的周长=2 πr。如果我们能使D点落在任意一个圆的周长的单位长度上的概率相等,即可使圆内概率相等。简单的说,如果有一个随机生成器取r的概率和r线性相关,就可以搞定这个问题。
构造如下的方法解决这个问题:
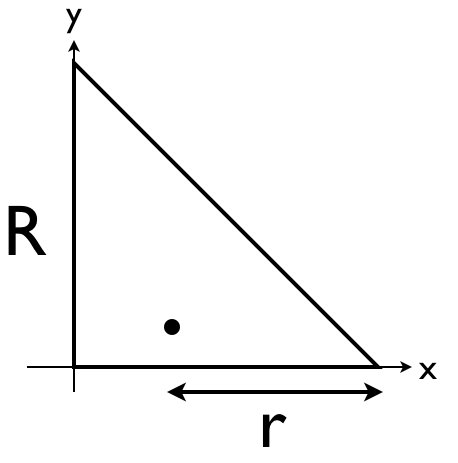
如图,构造一个边长为R的等腰直角三角形。使用等概率在三角形内生成一个点的方法生成D点。将R减D点的x坐标设置为r。
此时,r取值概率与r的大小线性相关,满足上面条件。因此,用此方法生成的点在圆内等概率分布。
2013年9月23日 10:55
为什么很大的页面,文章的宽度这么窄啊?能有办法调一下吗?
2013年9月23日 14:47
没有办法呀,主题就是这么蛋疼@kitt:
2013年9月23日 15:14
试一下Todo主题,“外观”的倒数第二个 @hustsxh:
2013年11月04日 00:06
CD = b(aAB+CA)
请问这公式是如何得知的?
2013年11月08日 18:51
@Rex: 这个是构造出来的,你在AB边上选一个点记为E,向量AE= alpha * 向量AB,向量CE = (alpha * 向量AB + 向量CA),然后就是 向量CD = beta * (alpha * 向量AB + 向量CA)了
2014年3月19日 00:04
显然应该用 rejection method,楼主在瞎搞。
2014年3月19日 09:06
楼主比较弱,学习了@uulm:
2015年3月10日 12:52
asd
2015年3月10日 12:55
我们认为,a和b是两个独立随机生成器(且范围都是[0,1]),那么三角形那里给出的第二个公式
三角形内取到的概率不是均匀的
2015年3月10日 13:24
@peter: 是的,这样做确实不均匀
2015年8月13日 00:50
不是轴对称,是中心对称
2023年4月24日 15:06
we are providing the pdf based on internet search according to past years old examination test and those question bank or study material download and shared based on the internet only.All the Users of the BoardModelPapers can use those <a href="http://boardmodelpaper.com/">boardmodelpaper.com</a> sample papers or Previous Paper Pdf of class-wise study material and blueprint and any for reference purpose only and we are providing the pdf based on internet search according to past years old examination test and those question bank.
2023年4月24日 15:08
we are providing the pdf based on internet search according to past years old examination test and those question bank or study material download and shared based on the internet only.All the Users of the BoardModelPapers can use those boardmodelpaper.com sample papers or Previous Paper Pdf of class-wise study material and blueprint and any for reference purpose only and we are providing the pdf based on internet search according to past years old examination test and those question bank.
2024年2月21日 21:10
Awesome blog. I enjoyed reading your articles. This is truly a great read for me. I have bookmarked it and I am looking forward to reading new articles. Keep up the good work