三角形内随机生成一个点

在三角形内生成一个点

已有一个能生成0到1之间的数，并且这些数是均匀分布的随机生成器，给定一个任意的三角形，如何能在三角形内随机的生成一个点？

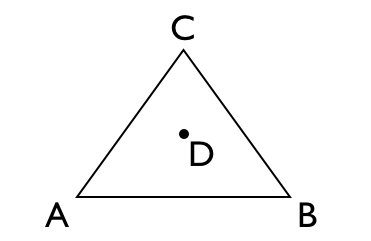
如上面这个三角形，点D就是三角形内部随机的一个点。一种简单的方法是通过如下公式生成D点：

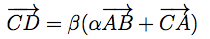或者

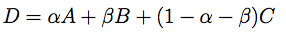
其中，a和b是两个独立随机生成器

要求等概率的情况

以上的两个公式很好的解决了在三角形内随机生成一个点的问题。然而三角形内每一个点被取到的概率一样吗？

拿

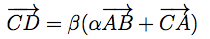
来说。a和b从0开始，每隔1/n取一个点。但n＝3时，a和b的取值为{0, 1/3, 2/3, 1}，将取到的D点在三角形种标出，如下图

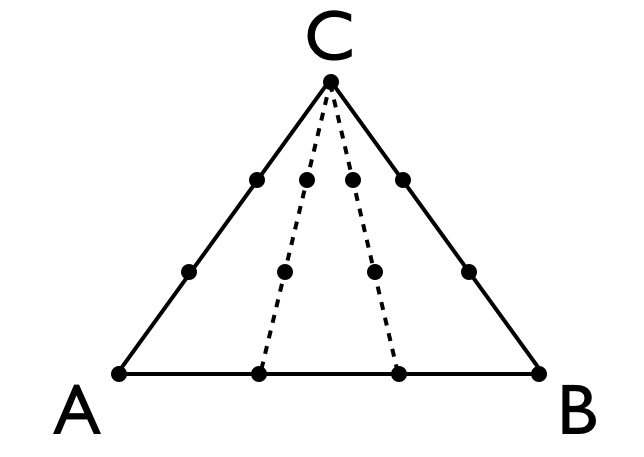
很明显，靠近C点的地方D取值的概率更大。但n趋近于正无穷的时候，上面的图就是D取值的概率密度函数。很显然，三角形内每一个点被取到的概率并不相等。

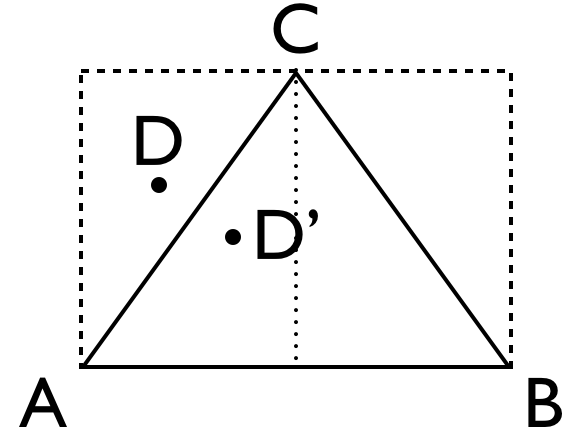
为了克服这个问题，一名睿智的同学提出了如下的方法：

1. 将三角形扩充成一个矩形

2. 将矩形的两条边分别线性映射成一个随机生成器，这两个随机生成器相互独立

3. 如果生成的D点在三角形外，将D以靠近的边为对称轴映射到三角形内的D'上。

显然随机生成的点在矩形内的分布是等概率的，第3部的映射也是一一对应的，因此在三角形内生成的点也是均匀分布的。

多边形内随机生成一个点

多边形可以先分割成多个三角形。根据面积的比率，使用一次随机生成器确定点落在哪个三角形内。然后在使用上面的方法在三角形内随机生成一个点。

圆内随机生成一个点

给定一个半径为R的圆，如何在圆内等概率随机生成一个点？

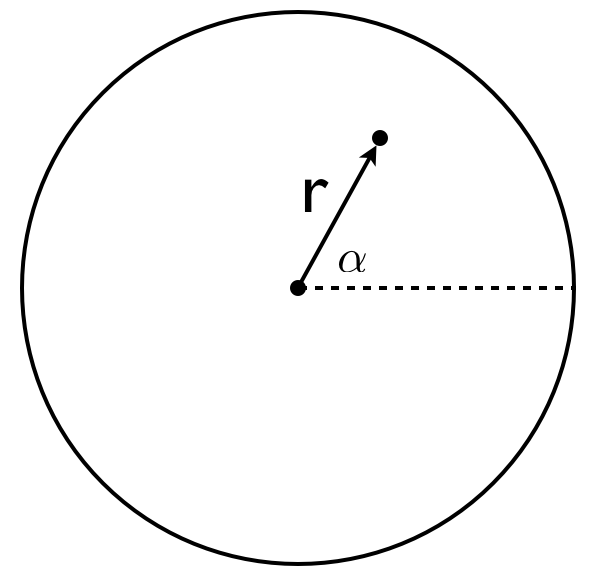
圆用笛卡尔坐标系很不好处理，自然想到使用极坐标系。a表示OD与极轴的夹角，r表示D到坐标原点的距离。a从0度到360度，r从0到R。

如果将a和r直接线性映射到两个独立的随机生成器上。很明显圆内的概率密度函数并不相等。

当r为一个定值，D的轨迹为一个圆，圆的周长＝2 πr。如果我们能使D点落在任意一个圆的周长的单位长度上的概率相等，即可使圆内概率相等。简单的说，如果有一个随机生成器取r的概率和r线性相关，就可以搞定这个问题。

构造如下的方法解决这个问题：

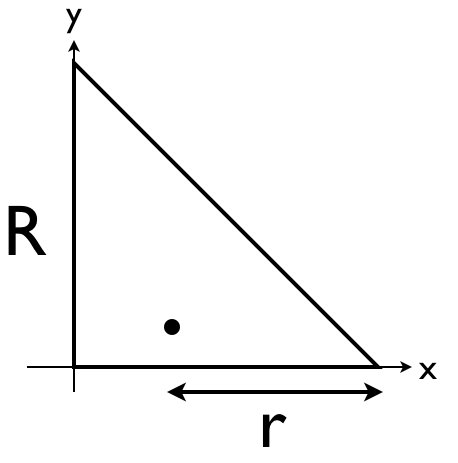
如图，构造一个边长为R的等腰直角三角形。使用等概率在三角形内生成一个点的方法生成D点。将R减D点的x坐标设置为r。

此时，r取值概率与r的大小线性相关，满足上面条件。因此，用此方法生成的点在圆内等概率分布。