题目大意

已知斐波那契数列F1 = 1, F2 = 2, Fi = Fi - 1 + Fi - 2 (i > 2)。定义Ai(k) = Fi × ik (i ≥ 1)，求A1(k) + A2(k) + ... + An(k)对1000000007(10⁹+7)取模的结果。(1 ≤ n ≤ 1017; 1 ≤ k ≤ 40)

题目链接： http://codeforces.com/problemset/problem/392/C

解题报告

算法思路

这类题目基本上都是矩阵快速幂。

分析流程

1. 二项式

首先根据二项式定理

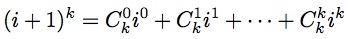
可以得到以下等式

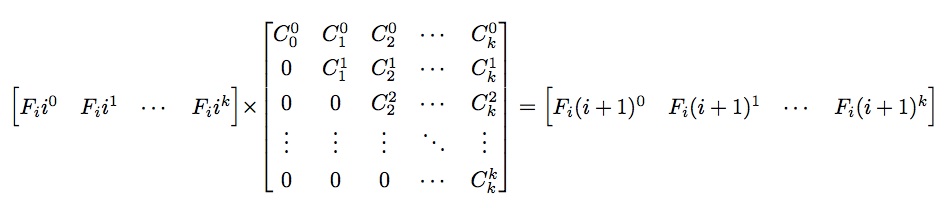
2. 简写

为了方便后续公式的书写，我们做如下定义（简写），记

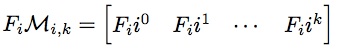
于是上面的公式可以简写为如下形式：

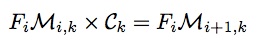
3. 矩阵构造

根据题目意思，令

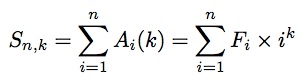
同时定义一个 k乘1的列向量，该列向量前k－1行均为0，最后一行为1，记为Ik

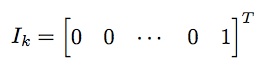
构造如下矩阵，根据前面简写、定义，可知如下等式成立。

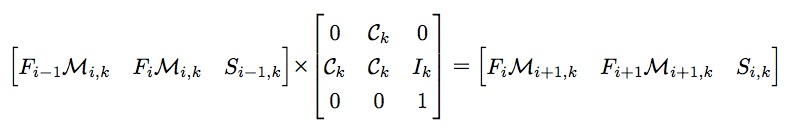
根据上述等式，很容易写出如下的通项公式

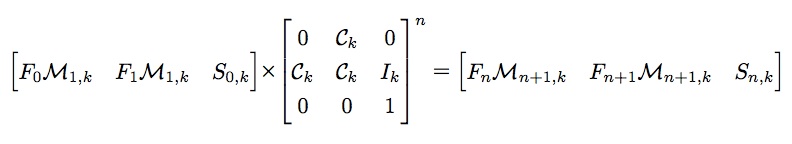
4. 初值

根据题目意思，斐波那契数列初值F1 = 1, F2 = 2，可以推断F0 = 1，于是通项公式的初值如下：

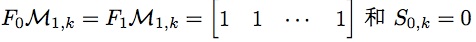
5. 求解

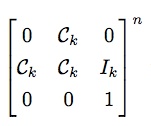部分由矩阵快速幂求解。时间复杂度为O((2k + 3)³ log n)=O(k³ log n)。矩阵快速幂后乘以初值即可得到答案。

代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>

using namespace std;

typedef long long LL;

#define maxn 84
#define MOD 1000000007

LL A[maxn][maxn], C[41][41], ans[maxn][maxn], tp[maxn][maxn];

void gen(int k) {
    for (int i = 0; i <= k; ++i) {
        C[i][0] = C[i][i] = 1;
    }
    for (int i = 2; i <= k; ++i) {
        for (int j = 1; j < i; ++j) {
            C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % MOD;
        }
    }
    for (int i = 0; i <= k; ++i) {
        for (int j = i; j <= k; ++j) {
            A[i + k + 1][j] = A[i][j + k + 1] = A[i + k + 1][j + k + 1] = C[j][i];
        }
    }
    A[2 * k + 1][2 * k + 2] = 1;
    A[2 * k + 2][2 * k + 2] = 1;
    
    for (int i = 0; i < 2 * k + 3; ++i) {
        ans[i][i] = 1;
    }
}

void multi(LL C[][maxn], LL A[][maxn], LL B[][maxn], int n) {
    memset(tp, 0, sizeof(tp));
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            for (int k = 0; k < n; ++k) {
                tp[i][j] = (tp[i][j] + A[i][k] * B[k][j] % MOD) % MOD;
            }
        }
    }
    memcpy(C, tp, sizeof(tp));
}

LL solve(LL n, int k) {
    gen(k);
    
    while (n) {
        if (n % 2) {
            multi(ans, A, ans, 2 * k + 3);
        }
        multi(A, A, A, 2 * k + 3);
        n /= 2;
    }
    
    LL res = 0;
    for (int i = 0; i < 2 * k + 2; ++i) {
        res = (res + ans[i][2 * k + 2]) % MOD;
    }
    return res;
}

int main() {
    LL n;
    int k;
    cin >> n >> k;
    
    cout << solve(n, k) << endl;
    

    return 0;
}

• 相关文章
• 全局相关文章