codeforces 392 c Yet Another Number Sequence
2014年2月20日 00:31
题目大意
已知斐波那契数列F1 = 1, F2 = 2, Fi = Fi - 1 + Fi - 2 (i > 2)。定义Ai(k) = Fi × ik (i ≥ 1),求A1(k) + A2(k) + ... + An(k)对1000000007(109+7)取模的结果。(1 ≤ n ≤ 1017; 1 ≤ k ≤ 40)
题目链接: http://codeforces.com/problemset/problem/392/C
解题报告
算法思路
这类题目基本上都是矩阵快速幂。
分析流程
1. 二项式
首先根据二项式定理
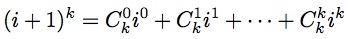
可以得到以下等式
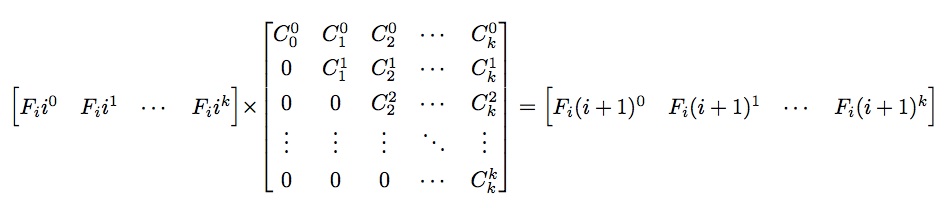
2. 简写
为了方便后续公式的书写,我们做如下定义(简写),记
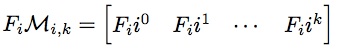

于是上面的公式可以简写为如下形式:
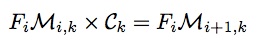
3. 矩阵构造
根据题目意思,令
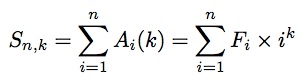
同时定义一个 k乘1的列向量,该列向量前k-1行均为0,最后一行为1,记为Ik
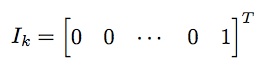
构造如下矩阵,根据前面简写、定义,可知如下等式成立。
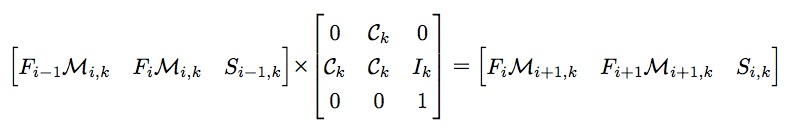
根据上述等式,很容易写出如下的通项公式
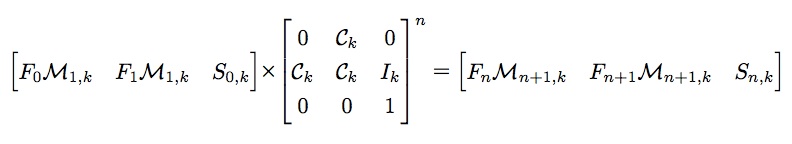
4. 初值
根据题目意思,斐波那契数列初值F1 = 1, F2 = 2,可以推断F0 = 1,于是通项公式的初值如下:
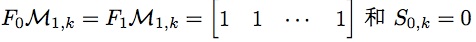
5. 求解
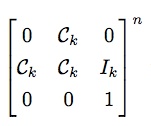 部分由矩阵快速幂求解。时间复杂度为O((2k + 3)3 log n)=O(k3 log n)。矩阵快速幂后乘以初值即可得到答案。
部分由矩阵快速幂求解。时间复杂度为O((2k + 3)3 log n)=O(k3 log n)。矩阵快速幂后乘以初值即可得到答案。
代码
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>
using namespace std;
typedef long long LL;
#define maxn 84
#define MOD 1000000007
LL A[maxn][maxn], C[41][41], ans[maxn][maxn], tp[maxn][maxn];
void gen(int k) {
for (int i = 0; i <= k; ++i) {
C[i][0] = C[i][i] = 1;
}
for (int i = 2; i <= k; ++i) {
for (int j = 1; j < i; ++j) {
C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % MOD;
}
}
for (int i = 0; i <= k; ++i) {
for (int j = i; j <= k; ++j) {
A[i + k + 1][j] = A[i][j + k + 1] = A[i + k + 1][j + k + 1] = C[j][i];
}
}
A[2 * k + 1][2 * k + 2] = 1;
A[2 * k + 2][2 * k + 2] = 1;
for (int i = 0; i < 2 * k + 3; ++i) {
ans[i][i] = 1;
}
}
void multi(LL C[][maxn], LL A[][maxn], LL B[][maxn], int n) {
memset(tp, 0, sizeof(tp));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
for (int k = 0; k < n; ++k) {
tp[i][j] = (tp[i][j] + A[i][k] * B[k][j] % MOD) % MOD;
}
}
}
memcpy(C, tp, sizeof(tp));
}
LL solve(LL n, int k) {
gen(k);
while (n) {
if (n % 2) {
multi(ans, A, ans, 2 * k + 3);
}
multi(A, A, A, 2 * k + 3);
n /= 2;
}
LL res = 0;
for (int i = 0; i < 2 * k + 2; ++i) {
res = (res + ans[i][2 * k + 2]) % MOD;
}
return res;
}
int main() {
LL n;
int k;
cin >> n >> k;
cout << solve(n, k) << endl;
return 0;
}