要准备找工作了，这几天在看july整理的面试题目，很全很强大。其中有个搜狗校招的笔试题目，觉得很有意思。思考了下，感觉相比给出的方法还有更好的方法。

题目

N个整数（数的大小为0-255）的序列，把它们加密为K个整数（数的大小为0-255）.再将K个整数顺序随机打乱，使得可以从这乱序的K个整数中解码出原序列。设计加密解密算法,且要求K<=15*N. 如果是：

1. N<=16,要求K<=16*N.
2. N<=16,要求K<=10*N.
3. N<=64,要求K<=15*N

第1、2问

因为N条件相同，所以第1问和第2问其实是同一个问题，解决了第2问也就搞定了第1问。

简单方法

原理

应题目要求，加密后的K个整数打乱顺序后还要能恢复原文，那么就需要将原文整数的位置信息也编码进密文。

一种简单的方法就是把密文的8位数分成3段

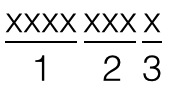
第1部分编码位置，N<=16的情况需要4位来表示
第2部分编码整数的第几位，000表示第0位，111表示第7位
第3部分编码某一位上的数值，如：0110 101 1表示，第6个数的第5位为1

原文整数范围[0-255]有8位，因此编码1个原文数字需要8个密文整数，即 K<=8N。已经可以满足第1、2问的要求了。

栗子

假设原文第6个整数为77，二进制表示为 01001101，那么可以编码成

0110 111 0
0110 110 1
0110 101 0
0110 100 0
0110 011 1
0110 010 1
0110 001 0
0110 000 1

好一点的方法

原理

这里我想到了一种更好一点的方法，可以使 K<=4N

首先，我们将原文整数写成4进制：x = a₃ * 64 + a₂ * 16 + a₁ * 4 + a₀(也就是将原文整数分为4段，每段2位)，记系数为a_i。由于i属于{0, 1, 2, 3}并且a_i也属于{0, 1, 2, 3}，因此我们考虑用2位编码i，2位编码a_i。于是密文的数字就被分为了这么三段

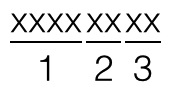
第1部分依然编码位置
第2部分编码i
第3部分编码a_i

这样只需要4个密文整数就可以编码一个原文整数了，即 K<=4N

栗子

假设原文第6个数字为77，二进制表示为 01001101，那么可以编码成

0110 11 01
0110 10 00
0110 01 11
0110 00 01

第三问

好一点的方法

原理

由于N<=64这样就必须用6位来编码位置，剩下只有2位来编码数值了。

继承第1、2问好一点的方法，我们用剩下的2位编码i，用出现的次数编码 a_i。也就是a_i等于多少对应的密文整数就出现多少次。由于i有4个，a_i<=3，故每一个原文整数最多需要4*3=12个密文整数来编码，也就是 K<=12N

栗子

假设原文第6个数字为77，二进制表示为 01001101，那么可以编码成

000110 11
000110 01
000110 01
000110 01
000110 00

更好一点的方法

原理

假设每1个原文整数最多能使用 n 个密文整数来编码。

对于1个密文数字依然需要6位来编码位置，剩下2位来编码数值信息。2位对应4个状态(00, 01, 10, 11)。n 个密文整数分给4个状态，状态出现的次数可以位0，并且n可以不用完。相当于5个状态分n个整数，最后一个状态表示没有用完的整数。则一共有C(n+4, 4)种组合方式。

我们用1种组合方式编码1个数值，[0-255]共有256个数值。那么要求满足 C(n+4, 4) >= 256。求的当n=7时，C(n+4,4)=330 > 256。故这种编码方式可以使得 K<=7N。状态对应的表格在这里下载

栗子

假设原文第6个数字为77，二进制表示为 01001101，那么可以编码成

000110 10
000110 10
000110 01
000110 01
000110 00
000110 00